How can a single theorem connect two of the most fundamental concepts in calculus—differentiation and integration? The Fundamental Theorem of Calculus does exactly that, serving as the bridge between these two pillars of mathematics. Without it, solving real-world problems involving motion, area, or rates of change would be far more complex.
Whether you’re a student struggling to grasp the basics or someone curious about how calculus shapes the world around us, this guide will break down the Fundamental Theorem of Calculus in a way that’s easy to understand. For example, imagine trying to calculate the displacement of a car over time using its velocity function. Once you learn calculus and understand this theorem, solving such real-world problems becomes not only possible but intuitive. By the end of this guide, you’ll know what the theorem is and how it applies to everything from physics to economics.
Let’s dive in!
Key Takeaways - Fundamental Theorem of Calculus
- The Fundamental Theorem of Calculus connects differentiation and integration, making it a cornerstone of calculus.
- The first fundamental theorem of calculus calculates definite integrals using antiderivatives.
- The second fundamental theorem of calculus shows that differentiation and integration are inverse processes.
- Real-world applications include physics, engineering, and economics.
- Tools like a fundamental theorem of calculus calculator can help verify your solutions.
What Is the Fundamental Theorem of Calculus?
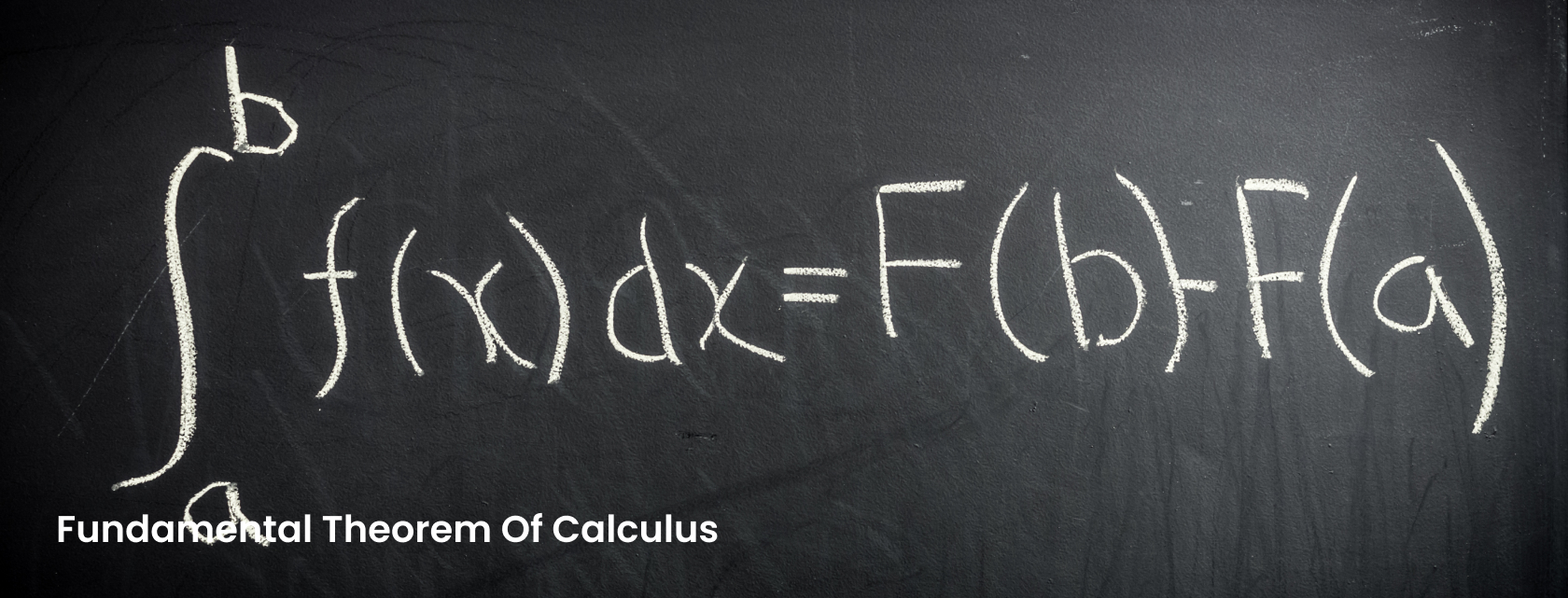
The Fundamental Theorem of Calculus establishes the relationship between differentiation and integration, two core concepts in calculus. It consists of two parts:
The First Fundamental Theorem of Calculus
The first fundamental theorem of calculus states that if a function is continuous on a closed interval [a,b][a, b][a,b], and F(x)F(x)F(x) is its antiderivative, then the definite integral of the function can be calculated as:
∫abf(x) dx=F(b)−F(a)\int_a^b f(x) \, dx = F(b) – F(a) ∫abf(x)dx=F(b)−F(a)
This means that instead of calculating the area under a curve manually, you can use the antiderivative to find the result quickly.
The Second Fundamental Theorem of Calculus
The second fundamental theorem of calculus states that if f(x)f(x)f(x) is a continuous function on an interval, then the derivative of its integral function is equal to the original function:
ddx(∫axf(t) dt)=f(x)\frac{d}{dx} \left( \int_a^x f(t) \, dt \right) = f(x) dxd(∫axf(t)dt)=f(x)
This part shows how differentiation and integration are inverse processes.
Why Is the Fundamental Theorem of Calculus Important?

The Fundamental Theorem of Calculus is crucial because it simplifies complex calculations. Instead of manually summing up areas or solving rates of change, the theorem provides a systematic way to solve these problems using antiderivatives and derivatives.
Real-World Applications:
- Physics: Calculating motion, velocity, and acceleration.
- Engineering: Analyzing forces and energy in structures.
- Economics: Determining cost and revenue functions.
By understanding the fundamental theorem of calculus formula, you can solve problems in various fields with ease.
Breaking Down the Fundamental Theorem of Calculus
To make the theorem easier to understand, let’s break it into smaller steps:
Step 1: Understanding the Antiderivative
The antiderivative is the reverse process of differentiation. For example, if f(x)=2xf(x) = 2xf(x)=2x, its antiderivative is F(x)=x2+CF(x) = x^2 + CF(x)=x2+C, where CCC is the constant of integration.
Step 2: Applying the First Fundamental Theorem
To calculate the definite integral of f(x)f(x)f(x) over [a,b][a, b][a,b], find the antiderivative F(x)F(x)F(x) and evaluate it at the endpoints:
∫13(2x) dx=F(3)−F(1)=(32)−(12)=9−1=8\int_1^3 (2x) \, dx = F(3) – F(1) = (3^2) – (1^2) = 9 – 1 = 8 ∫13(2x)dx=F(3)−F(1)=(32)−(12)=9−1=8
Step 3: Using the Second Fundamental Theorem
If you have an integral function like ∫0x(2t) dt\int_0^x (2t) \, dt∫0x(2t)dt, the derivative of this function is simply the original function:
ddx(∫0x(2t) dt)=2x\frac{d}{dx} \left( \int_0^x (2t) \, dt \right) = 2x dxd(∫0x(2t)dt)=2x
These steps show how the first fundamental theorem of calculus and the second fundamental theorem of calculus work together.
Applications of the Fundamental Theorem of Calculus

The Fundamental Theorem of Calculus has numerous applications in real-world scenarios. Here are a few examples:
Physics
- Calculating the displacement of an object using velocity functions.
- Determining the total work done by a force over a distance.
Engineering
- Analyzing stress and strain in materials.
- Calculating energy consumption in electrical circuits.
Economics
- Finding the total cost or revenue over a specific time period.
- Analyzing marginal cost and marginal revenue functions.
These fundamental theorem of calculus examples highlight its importance in solving practical problems.
Common Mistakes When Learning the Fundamental Theorem of Calculus
Many students struggle with the proof of the fundamental theorem of calculus or applying it correctly. Here are some common mistakes and how to avoid them:
- Forgetting the Constant of Integration: Always include CCC when finding the antiderivative.
- Misinterpreting the Limits of Integration: Ensure you evaluate the antiderivative at the correct endpoints.
- Confusing the Two Parts of the Theorem: Remember that the first part deals with definite integrals, while the second part connects derivatives and integrals.
Using a fundamental theorem of calculus calculator can help you verify your answers and avoid errors.
Conclusion - Mastering the Fundamental Theorem of Calculus
The Fundamental Theorem of Calculus is a cornerstone of mathematics, connecting differentiation and integration in a way that simplifies problem-solving. By understanding its two parts and practicing with examples, you can master this essential concept.
Whether you’re a student or a professional, learning the fundamental theorem of calculus formula will open doors to solving real-world problems in physics, engineering, and beyond. Ready to take your learning to the next level? Explore courses on FastLearner, the top e-learning platform, to deepen your understanding of calculus and other subjects.
FAQs About The Fundamental Theorem of Calculus
What is the first fundamental theorem of calculus?
The first fundamental theorem of calculus states that the definite integral of a function over an interval [a,b][a, b][a,b] can be calculated using its antiderivative: ∫abf(x) dx=F(b)−F(a)\int_a^b f(x) \, dx = F(b) – F(a)∫abf(x)dx=F(b)−F(a).
What is the first principle of the calculus equation?
The first principle of calculus refers to the definition of a derivative as the limit of the average rate of change:
f′(x)=limh→0f(x+h)−f(x)h.f'(x) = \lim_{h \to 0} \frac{f(x + h) – f(x)}{h}. f′(x)=h→0limhf(x+h)−f(x).
It forms the foundation of differentiation.
Who invented first principles calculus?
Sir Isaac Newton and Gottfried Wilhelm Leibniz, who are credited as the co-founders of modern calculus, developed the concept of first principles in calculus.
What is the first principle of the calculus equation?
The first principle of the calculus equation is the mathematical definition of a derivative, which calculates the instantaneous rate of change of a function at a specific point. It is derived using limits.



